Feedforward Deep Neural Networks

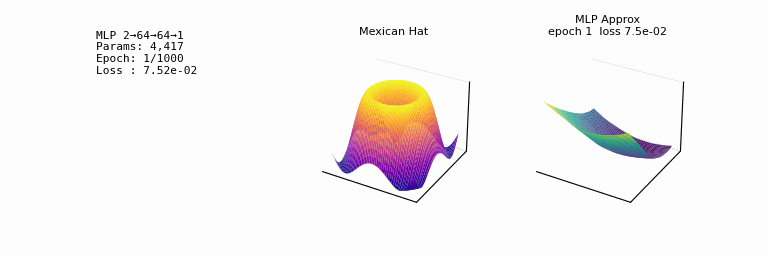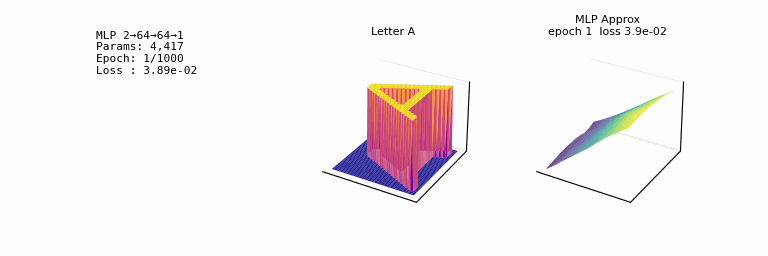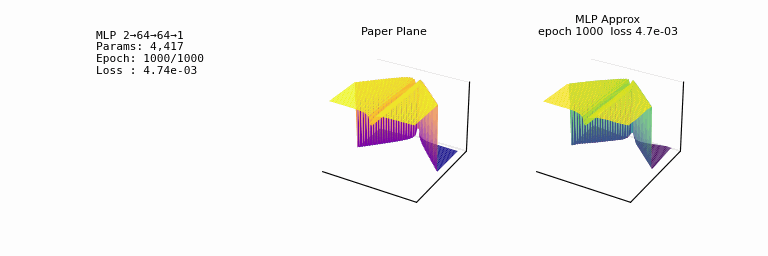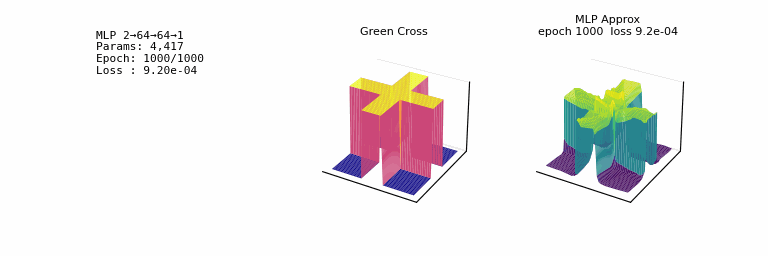
• one of the most striking facts about neural networks is that they can compute any function. 𐃏
• we will always be able to do better than some given error \(\epsilon\)
• what’s even crazier is that this universality holds even if we restrict our networks to just have a single layer intermediate between the input and output neurons:

• one of the original papers publishing this result leveraged the Hahn-Banach Theorem, the Riesz Representation theorem and some Fourier Analysis!

  Read more >

• given the findings of the previous chapter (universality), why would we concern ourselves with learning deep neural nets?
  • especially given that we are guaranteed to be able to approximate any function with just a single layer of hidden neurons?

well, just because something is possible, it doesn’t mean it’s a good idea!

considering that we are using computers, it’s usually a good idea to break the problem down into smaller sub-problems, solve those, and then come back to solve the main problem.

notes#

• topics: convolutions, pooling, GPUs (to do more training), algorithmic expansion of data (reduce overfitting), dropout (also reduce overfitting), ensembles of networks

  Read more >

3.1 the cross entropy function#

• we often learn fastest when we’re badly wrong about something
• the cross-entropy cost function is always negative (which is something you desire for a cost function)

\begin{equation} \label{eq:neuron_ce} C = -\frac{1}{n}\sum_x [y \ln a + (1-y)\ln(1-a)] \end{equation}

• note here that at a = 1, you’ll get nan. we handle this in the code below.
• this cost tends towards zero as the neuron gets better at computing the desired output y
• it also punishes bad guesses more harshly.
• the cross-entropy is nearly always the better choice, provided the output neurons are sigmoid neurons
• if the output neurons however are linear neurons, then the quadratic cost will not cause learning slowdown. you may use it.
• to find the learning rate \(\eta\) for log-reg, you can divide that of the lin-reg by 6.
• ch1 = 95.42 accuracy
• 100 hidden neurons \(\implies\) 96.82 percent.
  • eliminated one in fourteen errors; pretty good!
• neuron saturation is an important problem in neural nets.
• cross-entropy is a measure of surprise
  • ch5 Cover & Thomas
• a softmax output layer with log-likelihood cost is quite similar to a sigmoid output layer with cross-entropy cost.
• softmax plus log-likelihood is worth using whenever you want to interpret the output activations as probabilities.

3.2 overfitting and regularisation#

• the algorithm was introduced in the 1970s, but its importance wasn’t fully appreciated until the famous 1986 paper by David Rumelhart, Geoffrey Hinton, and Ronald Williams.
• “workhorse of learning in neural networks”
• at the heart of it is an expression that tells us how quickly the cost function changes when we change the weights and biases.

notes#

• insight is forever
• his code is written in python 2.7
• emotional commitment is a key to achieving mastery

• primary visual cortex has 140 million neurons
• two types of artificial neuron: perceptron, sigmoid neuron
• perceptron takes binary inputs and produces a single binary output.
• perceptrons should be considered as making decisions after weighing up evidence (inputs)
• neural nets can express NAND, which means any computation can be built using these gates!

sigmoid neurons#

• you want to tweak the weights and biases such that small changes in either will produce a small change in the output
• as such we must break free from the sgn step function and introduce the sigmoid function