Personal Motivations

I grew up as a child with this puzzle in my house. My mother could solve it, along with a couple members on her side of the family.

Mum never knew the algorithm, nor any techniques beyond "My hand just knows"; as a result I spent 4 determined days in my youth working it until I had solved it.

/projects/csp/peg-solitaire/ coffee-pegs.jpg
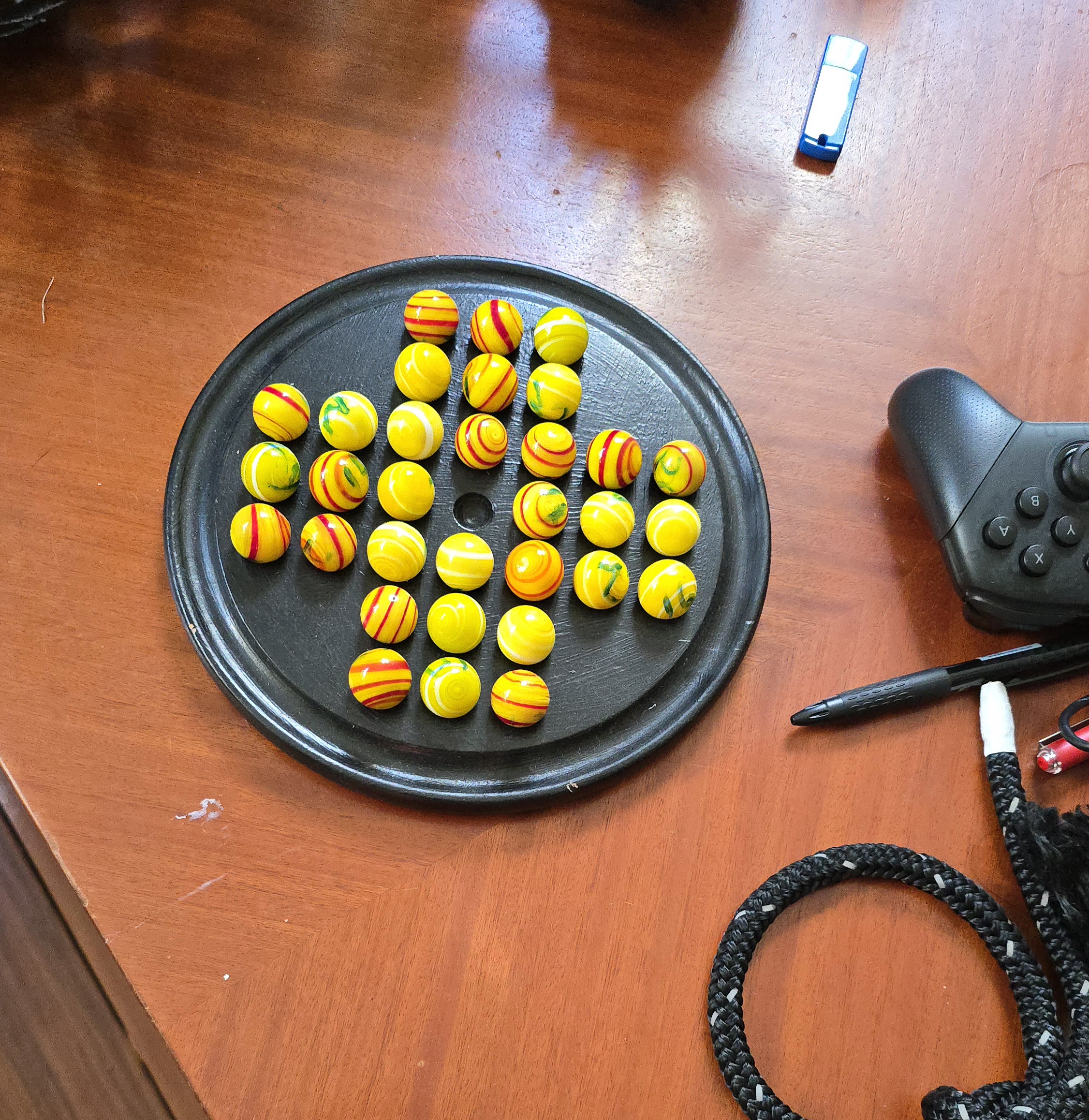
the one on my own coffee table

During these 4 days, I learned a heuristic: to consider the L shape `___|` and realise that for every such set, you can perform legal operations until you are left with a single marble. Then, since there are 32 marbles, you can do this 8 times until you have 4 remaining, and finally perform this "L-trick" one last time til a single peg remains in the middle of the board.

\[\begin{matrix} & & \mathrm{o} & \mathrm{o} & \mathrm{o} & & \\ & & \mathrm{o} & \mathrm{o} & \mathrm{o} & & \\ \mathrm{o} & \mathrm{o} & \mathrm{o} & \mathrm{o} & \mathrm{o} & \mathrm{o} & \mathrm{o} \\ \mathrm{o} & \mathrm{o} & \mathrm{o} & . & \mathrm{o} & \mathrm{o} & \mathrm{o} \\ \mathrm{o} & \mathrm{o} & \mathrm{o} & \mathrm{o} & \mathrm{o} & \mathrm{o} & \mathrm{o} \\ & & \mathrm{o} & \mathrm{o} & \mathrm{o} & & \\ & & \mathrm{o} & \mathrm{o} & \mathrm{o} & & \\ \end{matrix}\;\leadsto\;\begin{matrix} & & \cdot & \cdot & \cdot & & \\ & & \cdot & \cdot & \cdot & & \\ \cdot & \cdot & \cdot & . & \cdot & \cdot & \cdot \\ \cdot & \cdot & \cdot & \mathrm{o} & \cdot & \cdot & \cdot \\ \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot \\ & & \cdot & \cdot & \cdot & & \\ & & \cdot & \cdot & \cdot & & \\ \end{matrix}\]

start board to end board

Pin the Name to the Puzzle

After battling hard for this solution, I quickly lost the exact set of moves I had performed to obtain the solution.

Following a little more perseverance I had begun to solve the puzzle by via a new auxillary method each time—the common denominator amongst all these being—"use the L-shape".

I finally decide to begin Googling for "marble puzzle" and "board puzzle with marbles", etc. Because at the time I hadn't a clue what the puzzle was called!

Eventually I discover the wikipedia page and learn that there are upward of 18,000 distinct solutions. Hilarious in retrospect, and made me wonder at the time how I didn't even accidentally win!

A few years later, (British)

Life takes a few twists and turns, but eventually I end up amongst a serious study of Computer Science and Algorithms. Equipped now with the ability to write Python code, I first reproduce the Game itself in code.

Single-Player, Board + Play Code 

#import numpy as np
from os import system

P = 99 # player is 99
N = 7 # board width

board = [[ 0,  0,  1,  2,  3,  0,  0],
         [ 0,  0,  4,  5,  6,  0,  0],
         [ 7,  8,  9, 10, 11, 12, 13],
         [14, 15, 16, -1, 17, 18, 19],
         [20, 21, 22, 23, 24, 25, 26],
         [ 0,  0, 27, 28, 29,  0,  0],
         [ 0,  0, 30, 31, 32,  0,  0]]

empties = []
jumplist = []
valids = 0

class Player:
    def __init__(self):
        self.position = [3, 3]
        self.moves = []

    def move(self, m):
        match m:
            case "w":
                if (self.position[0] > 0 
                        and board[self.position[0]-1][self.position[1]] != 0):
                    self.position[0] -= 1
            case "a":
                if (self.position[1] > 0
                        and board[self.position[0]][self.position[1]-1] != 0):
                    self.position[1] -= 1
            case "s":
                if (self.position[0] < N-1
                        and board[self.position[0]+1][self.position[1]] != 0):
                    self.position[0] += 1
            case "d":
                if (self.position[1] < N-1
                        and board[self.position[0]][self.position[1]+1] != 0):
                    self.position[1] += 1
            case " ":
                self.jump(input("jump where? "))

    def jump(self, j):
        match j:
            case "w":
                if (self.position[0] > 1 
                        and board[self.position[0]-1][self.position[1]] > 0
                        and board[self.position[0]-2][self.position[1]] < 0):
                    empties.append(board[self.position[0]-1][self.position[1]])
                    empties.append(board[self.position[0]][self.position[1]])
                    jumplist.append([board[self.position[0]][self.position[1]], "w"])
                    board[self.position[0]-1][self.position[1]] = -1
                    board[self.position[0]-2][self.position[1]] = board[self.position[0]][self.position[1]]
                    board[self.position[0]][self.position[1]] = -1
                    self.position[0] -= 2
            case "a":
                if (self.position[1] > 1
                        and board[self.position[0]][self.position[1]-2] < 0
                        and board[self.position[0]][self.position[1]-1] > 0):
                    empties.append(board[self.position[0]][self.position[1]-1])
                    empties.append(board[self.position[0]][self.position[1]])
                    jumplist.append([board[self.position[0]][self.position[1]], "a"])
                    board[self.position[0]][self.position[1]-1] = -1
                    board[self.position[0]][self.position[1]-2] = board[self.position[0]][self.position[1]]
                    board[self.position[0]][self.position[1]] = -1
                    self.position[1] -= 2
            case "s":
                if (self.position[0] < N-2
                        and board[self.position[0]+2][self.position[1]] < 0
                        and board[self.position[0]+1][self.position[1]] > 0):
                    empties.append(board[self.position[0]+1][self.position[1]])
                    empties.append(board[self.position[0]][self.position[1]])
                    jumplist.append([board[self.position[0]][self.position[1]], "s"])
                    board[self.position[0]+1][self.position[1]] = -1
                    board[self.position[0]+2][self.position[1]] = board[self.position[0]][self.position[1]]
                    board[self.position[0]][self.position[1]] = -1
                    self.position[0] += 2
            case "d":
                if (self.position[1] < N-2
                        and board[self.position[0]][self.position[1]+2] < 0
                        and board[self.position[0]][self.position[1]+1] > 0):
                    empties.append(board[self.position[0]][self.position[1]+1])
                    empties.append(board[self.position[0]][self.position[1]])
                    jumplist.append([board[self.position[0]][self.position[1]], "d"])
                    board[self.position[0]][self.position[1]+1] = -1
                    board[self.position[0]][self.position[1]+2] = board[self.position[0]][self.position[1]]
                    board[self.position[0]][self.position[1]] = -1
                    self.position[1] += 2


def print_board(player):
    for i, row, in enumerate(board):
        for col in range(len(row)):
            if ([i,col] == player.position):
                print('X', end='')
            elif (row[col] > 0):
                print('.', end='')
            elif (row[col] == 0):
                print(' ', end='')
            elif (row[col] < 0):
                print('O', end='')
        print('\n')
    print("empties: ", empties)
    print("jumplist: ", jumplist)
    print("valids: ", valids)

def check_loss():
    global valids
    valids = 0
    for i, row in enumerate(board):
        for col in range(len(row)):
            if ((i > 1 and board[i-2][col] < 0 and board[i-1][col] > 0) or 
                (col > 1 and board[i][col-2] < 0 and board[i][col-1] > 0) or 
                (i < N-2 and board[i+2][col] < 0 and board[i+1][col] > 0) or
                    (col < N-2 and board[i][col+2] < 0 and board[i][col+1] > 0)):
                if (board[i][col] > 0):
                    valids += 1
    if (valids == 0):
        game_over(0)


def check_win():
    pegs = 0
    for i, row in enumerate(board):
        for col in range(len(row)):
            if (board[i][col] > 0):
                pegs+= 1
        if (pegs > 1):
            return
    if (pegs == 1):
        game_over(1)


def game():
    player = Player()
    print_board(player)
    print(player.position)
    while True:
        inp = input("move: ")
        if (inp == "q"):
            break
        player.move(inp)
        check_win()
        check_loss()
        system('clear')
        print_board(player)

def game_over(status):
    if (status == 1):
        print("GAME OVER: YOU WON!")
    else:
        print("GAME OVER: YOU LOST!")
    exit()
    

if __name__ == "__main__":
    game()
/projects/csp/peg-solitaire/ board-run.png
Figure 1: British Board

Running the program with python3.12 board.py yields Figure 1, where you move the X with WASD controls, and perform "jumps" with it by hitting <space> and a direction (WASD) to jump in. Furthermore, empties: is the list of empty pegs jumplist: is the list of jumps you performed valids: is the number of valid moves remaining move: takes in WASD or q for quit.

Depth-First Search (DFS) Code

Then, I write a little more code to play the game-in all its combinatorical vastness-for me, and output the solution:

EMPTY = -1
PEG = 1
VOID = 0
N = 7

class PegSolitaire:
    def __init__(self, board):
        self.board = board
        self.moves = []

    def is_solved(self):
        pegs = 0
        position = []
        for i, row in enumerate(board):
            for col in range(len(row)):
                if (board[i][col] > 0):
                    position.append([i, col])
                    pegs+= 1
            if (pegs > 1):
                return False
        if (pegs == 1 and position == [[3,3]]):
            return True

    def get_valid_moves(self):
        valids = []
        for i, row in enumerate(board):
            for col in range(len(row)):
                if (board[i][col] > 0):
                    if (i > 1 and board[i-2][col] < 0 and board[i-1][col] > 0):
                        valids.append([i,col,"w",board[i-1][col]])
                    elif (col > 1 and board[i][col-2] < 0 and board[i][col-1] > 0): 
                        valids.append([i,col,"a",board[i][col-1]])
                    elif (i < N-2 and board[i+2][col] < 0 and board[i+1][col] > 0):
                        valids.append([i,col,"s",board[i+1][col]])
                    elif (col < N-2 and board[i][col+2] < 0 and board[i][col+1] > 0):
                        valids.append([i,col,"d",board[i][col+1]])
        print("VALID MOVES:", valids)
        print("MOVES thus far:", self.moves)
        return valids

    def make_move(self, move):
        self.moves.append(move)
        match move[2]:
            case "w":
                board[move[0]-1][move[1]] = -1
                board[move[0]-2][move[1]] = board[move[0]][move[1]]
                board[move[0]][move[1]] = -1
                move[0] -= 2
            case "a":
                board[move[0]][move[1]-1] = -1
                board[move[0]][move[1]-2] = board[move[0]][move[1]]
                board[move[0]][move[1]] = -1
                move[1] -= 2
            case "s":
                board[move[0]+1][move[1]] = -1
                board[move[0]+2][move[1]] = board[move[0]][move[1]]
                board[move[0]][move[1]] = -1
                move[0] += 2
            case "d":
                board[move[0]][move[1]+1] = -1
                board[move[0]][move[1]+2] = board[move[0]][move[1]]
                board[move[0]][move[1]] = -1
                move[1] += 2
    
    def undo_move(self):
        move = self.moves.pop()
        print("POPPED:", move)
        match move[2]:
            case "w":
                board[move[0]+2][move[1]] = board[move[0]][move[1]]
                board[move[0]][move[1]] = -1
                board[move[0]+1][move[1]] = move[3]
            case "a":
                board[move[0]][move[1]+2] = board[move[0]][move[1]]
                board[move[0]][move[1]] = -1
                board[move[0]][move[1]+1] = move[3]
            case "s":
                board[move[0]-2][move[1]] = board[move[0]][move[1]]
                board[move[0]][move[1]] = -1
                board[move[0]-1][move[1]] = move[3]
            case "d":
                board[move[0]][move[1]-2] = board[move[0]][move[1]] 
                board[move[0]][move[1]] = -1
                board[move[0]][move[1]-1] = move[3]
    def solve(self):
        if self.is_solved():
            return True
        for move in self.get_valid_moves():
            self.print_board()
            self.make_move(move)
            if self.solve():
                return True
            self.undo_move()
        return False

    def print_moves(self):
        print(self.moves)
        print(len(self.moves))
            
    def print_board(self):
        for row in board:
            for col in range(len(row)):
                if (row[col] > 0):
                    print('.', end='')
                elif (row[col] == 0):
                    print(' ', end='')
                elif (row[col] < 0):
                    print('O', end='')
            print('\n')

if __name__ == "__main__":
    board = [[ 0,  0,  1,  2,  3,  0,  0],
             [ 0,  0,  4,  5,  6,  0,  0],
             [ 7,  8,  9, 10, 11, 12, 13],
             [14, 15, 16, -1, 17, 18, 19],
             [20, 21, 22, 23, 24, 25, 26],
             [ 0,  0, 27, 28, 29,  0,  0],
             [ 0,  0, 30, 31, 32,  0,  0]]
    game = PegSolitaire(board)
    game.solve()
    game.print_moves()

Here we use a naïve recursive backtracking depth-first-search to stitch together a list of valid and winning moves.

The algorithm can be summarised with this single code block from above:

    def solve(self):
        if self.is_solved():
            return True
        for move in self.get_valid_moves():
            self.make_move(move)
            if self.solve():
                return True
            self.undo_move()
        return False

Algorithmic Analysis.

/projects/csp/peg-solitaire/ naive-dfs.gif
Figure 2: Naïve DFS Gametree

Above, I call this implementation for DFS naïve. And I say this because our algorithm forces it's way through the game-tree and explores every move for every board state…

Including the board-states it has already visited!

This is by no means inherently bad. The solution gets found, but in a couple sections we will see that this technique no longer works.

In the figure to the right, you will see that the first move has 4 symmetric options, and each of these has 3 options which subsequently have 5 options each. I have only drawn the top-down tree for the first 3 levels (of 31), but it should be clear that duplicate board states will be re-explored and thus all their children board-states will also be expanded. This is terrible for the complexity for our algorithm, and as a consequence the current script takes approximately 2 minutes to run. The output of time python3.12 dfs.py is

python dfs.py  112.28s user 27.73s system 98% cpu 2:21.66 total

Mathematics

A peg is either in a slot or not in a slot. We have 33 slots, with 32 marbles.

At first I thought that there would be \({32\choose 33}\times 2^{32}\) combinations for this puzzle, however this is an underestimate of the real value.

The mistake in this line-of-thought is that we are arranging the 32 marbles in on/off pairs and then superimposing these onto the 33 peg board. This is incorrect, because any move should be able to "end up" on that 33rd peg, and so we should be flipping our bits on the full board.

As such, the correct calculation is to take all \(2^{33}\) combinations and then subtract off the 2 impossible cases:

  1. an entirely empty board
  2. an entirely filled board.

Thus the number of unique combinations of a combinatoric board is \[2^{32}-2 = 8,589,934,590\]

However, like in the analysis of the Rubik's Cube, our real-world puzzle has rules which further restrict permutations—we must leave the middle hole empty!

The code for the calculations below are out of the scope of this post, but if you wish to see how I have derived these values, you may view the cpp code on github.

Depth 0: 1 new unique state(s).
Depth 1: 4 new unique state(s).
Depth 2: 12 new unique state(s).
Depth 3: 60 new unique state(s).
Depth 4: 296 new unique state(s).
Depth 5: 1338 new unique state(s).
Depth 6: 5648 new unique state(s).
Depth 7: 21842 new unique state(s).
Depth 8: 77559 new unique state(s).
Depth 9: 249690 new unique state(s).
Depth 10: 717788 new unique state(s).
Depth 11: 1834379 new unique state(s).
Depth 12: 4138302 new unique state(s).
Depth 13: 8171208 new unique state(s).
Depth 14: 14020166 new unique state(s).
Depth 15: 20773236 new unique state(s).
Depth 16: 26482824 new unique state(s).
Depth 17: 28994876 new unique state(s).
Depth 18: 27286330 new unique state(s).
Depth 19: 22106348 new unique state(s).
Depth 20: 15425572 new unique state(s).
Depth 21: 9274496 new unique state(s).
Depth 22: 4792664 new unique state(s).
Depth 23: 2120101 new unique state(s).
Depth 24: 800152 new unique state(s).
Depth 25: 255544 new unique state(s).
Depth 26: 68236 new unique state(s).
Depth 27: 14727 new unique state(s).
Depth 28: 2529 new unique state(s).
Depth 29: 334 new unique state(s).
Depth 30: 32 new unique state(s).
Depth 31: 5 new unique state(s).

Finished BFS. Explored a total of 187636299 unique states overall.

Thus, \(187,636,299 \div 8,589,934,590 \approx 2.18\%\), and this is the percentage of Peg Solitaire boards to the total possible quantity of boards that exist.

Solution

Drunkenly, my program outputs [[3, 3, 's', 10], [2, 3, 'd', 9], [2, 2, 's', 4], [0, 2, 'a', 2], [2, 1, 'a', 1], [2, 2, 'd', 8], [0, 4, 'w', 6], [2, 4, 'a', 12], [1, 2, 'w', 7], [2, 2, 's', 16], [3, 2, 'd', 15], [1, 2, 'w', 3], [1, 4, 'w', 13], [2, 4, 's', 17], [3, 4, 'a', 18], [1, 4, 'w', 11], [3, 2, 'w', 22], [4, 2, 'd', 21], [2, 2, 'w', 27], [3, 2, 's', 20], [3, 4, 'd', 5], [2, 4, 'w', 14], [3, 4, 's', 24], [4, 4, 'a', 25], [4, 5, 'd', 26], [4, 4, 'w', 29], [5, 4, 's', 32], [6, 4, 'd', 31], [4, 4, 'w', 19], [4, 3, 'a', 30], [3, 3, 'w', 23]].

Which, for the first item translates to:

"perform the 's' move into coordinates (3,3)1, and kill marble 10"

However, I shall do you the service of interpolating a nicer, more human table of moves.

Consider first the representation of each peg's underlying slot as a number from 1 to 32:: \[\newline\begin{matrix} & & \mathrm{o} & \mathrm{o} & \mathrm{o} & & \\ & & \mathrm{o} & \mathrm{o} & \mathrm{o} & & \\ \mathrm{o} & \mathrm{o} & \mathrm{o} & \mathrm{o} & \mathrm{o} & \mathrm{o} & \mathrm{o} \\ \mathrm{o} & \mathrm{o} & \mathrm{o} & . & \mathrm{o} & \mathrm{o} & \mathrm{o} \\ \mathrm{o} & \mathrm{o} & \mathrm{o} & \mathrm{o} & \mathrm{o} & \mathrm{o} & \mathrm{o} \\ & & \mathrm{o} & \mathrm{o} & \mathrm{o} & & \\ & & \mathrm{o} & \mathrm{o} & \mathrm{o} & & \\ \end{matrix}\;\;\leadsto\;\;\begin{matrix} & & 1 & 2 & 3 & & \\ & & 4 & 5 & 6 & & \\ 7 & 8 & 9 & 10 & 11 & 12 & 13 \\ 14 & 15 & 16 & . & 17 & 18 & 19 \\ 20 & 21 & 22 & 23 & 24 & 25 & 26 \\ & & 27 & 28 & 29 & & \\ & & 30 & 31 & 32 & & \\ \end{matrix}\newline\]

Then we position our hand on marble \(n\), and execute moves u,d,l,r2.

\[\footnotesize\begin{array}{c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c} \mathrm{marble} & \mathrm{5} & \mathrm{8} & \mathrm{1} & \mathrm{3} & \mathrm{10} & \mathrm{7} & \mathrm{11} & \mathrm{13} & \mathrm{16} & \mathrm{1} & \mathrm{14} & \mathrm{16} & \mathrm{17} & \mathrm{3} & \mathrm{19} & \mathrm{17} & \mathrm{27} & \mathrm{20} & \mathrm{22} & \mathrm{4} & \mathrm{16} & \mathrm{24} & \mathrm{6} & \mathrm{26} & \mathrm{23} & \mathrm{32} & \mathrm{17} & \mathrm{30} & \mathrm{32} & \mathrm{25} & \mathrm{28} \\ \hline \mathrm{move} & \mathrm{d} & \mathrm{r} & \mathrm{d} & \mathrm{l} & \mathrm{l} & \mathrm{r} & \mathrm{u} & \mathrm{l} & \mathrm{u} & \mathrm{d} & \mathrm{r} & \mathrm{u} & \mathrm{u} & \mathrm{d} & \mathrm{l} & \mathrm{u} & \mathrm{u} & \mathrm{r} & \mathrm{u} & \mathrm{d} & \mathrm{r} & \mathrm{u} & \mathrm{d} & \mathrm{l} & \mathrm{r} & \mathrm{u} & \mathrm{d} & \mathrm{r} & \mathrm{u} & \mathrm{l} & \mathrm{u} \end{array}\]

English / British Solution

Yielding

/projects/csp/peg-solitaire/ british-solved.jpg
32 Peg Solitaire Solved

Kong Kong's European Version 💀

This section weaves a new narrative, one that begins with my own naïveté, and ends with significant refactorings of code.

I purchased this Peg Solitaire for a relative:

/projects/csp/peg-solitaire/ european.jpg
European Peg Solitaire

It was rather expensive, but it looked to be the only sensible choice on Amazon; so we bought it.

In reality, the marbles were more like planets, and the board some Chef Flambé's utensil. The puzzle was/is huge.

/projects/csp/peg-solitaire/ size.jpg
36 Marble Peg Solitaire
/projects/csp/peg-solitaire/ fair.jpg
the seller was honest

In addition to not realising that the board was 16 inches, I had also not realised that this puzzle was different to one I had grown up with!

This version contains 36 marbles with an extra marble at each corner. Creating a uniform staircase pattern all around the board:

\[\begin{matrix} & & \mathrm{o} & \mathrm{o} & \mathrm{o} & & \\ &\mathrm{o} & \mathrm{o} & \mathrm{o} & \mathrm{o} &\mathrm{o} & \\ \mathrm{o} & \mathrm{o} & \mathrm{o} & \mathrm{o} & \mathrm{o} & \mathrm{o} & \mathrm{o} \\ \mathrm{o} & \mathrm{o} & \mathrm{o} & \mathrm{o} & \mathrm{o} & \mathrm{o} & \mathrm{o} \\ \mathrm{o} & \mathrm{o} & \mathrm{o} & \mathrm{o} & \mathrm{o} & \mathrm{o} & \mathrm{o} \\ &\mathrm{o} & \mathrm{o} & \mathrm{o} & \mathrm{o} & \mathrm{o} & \\ & & \mathrm{o} & \mathrm{o} & . & & \\ \end{matrix}\;\leadsto\;\begin{matrix} & & \cdot & \cdot & \cdot & & \\ & \cdot& \cdot & \cdot & \cdot &\cdot & \\ \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot \\ \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot \\ \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot \\ &\cdot & \cdot & \cdot & \cdot &\cdot & \\ & & \cdot & \cdot & \mathrm{o} & & \\ \end{matrix}\]

Note the difference in starting position!

European, Single-Player, Board + Play (CODE)

I entirely skipped attempting this puzzle myself and fired up my Python interpreter:

#import numpy as np
from os import system

P = 99 # player is 99
N = 7 # board width

board = [[ 0,  0,  1,  2,  3,  0,  0],
         [ 0,  4,  5,  6,  7,  8,  0],
         [ 9, 10, 11, 12, 13, 14, 15],
         [16, 17, 18, 36, 19, 20, 21],
         [22, 23, 24, 25, 26, 27, 28],
         [ 0, 29, 30, 31, 32, 33,  0],
         [ 0,  0, 34, 35, -1,  0,  0]]

empties = []
jumplist = []
valids = 0

class Player:
    def __init__(self):
        self.position = [6, 4]
        self.moves = []

    def move(self, m):
        match m:
            case "w":
                if (self.position[0] > 0 
                        and board[self.position[0]-1][self.position[1]] != 0):
                    self.position[0] -= 1
            case "a":
                if (self.position[1] > 0
                        and board[self.position[0]][self.position[1]-1] != 0):
                    self.position[1] -= 1
            case "s":
                if (self.position[0] < N-1
                        and board[self.position[0]+1][self.position[1]] != 0):
                    self.position[0] += 1
            case "d":
                if (self.position[1] < N-1
                        and board[self.position[0]][self.position[1]+1] != 0):
                    self.position[1] += 1
            case " ":
                self.jump(input("jump where? "))

    def jump(self, j):
        match j:
            case "w":
                if (self.position[0] > 1 
                        and board[self.position[0]-1][self.position[1]] > 0
                        and board[self.position[0]-2][self.position[1]] < 0):
                    empties.append(board[self.position[0]-1][self.position[1]])
                    empties.append(board[self.position[0]][self.position[1]])
                    jumplist.append([board[self.position[0]][self.position[1]], "w"])
                    board[self.position[0]-1][self.position[1]] = -1
                    board[self.position[0]-2][self.position[1]] = board[self.position[0]][self.position[1]]
                    board[self.position[0]][self.position[1]] = -1
                    self.position[0] -= 2
            case "a":
                if (self.position[1] > 1
                        and board[self.position[0]][self.position[1]-2] < 0
                        and board[self.position[0]][self.position[1]-1] > 0):
                    empties.append(board[self.position[0]][self.position[1]-1])
                    empties.append(board[self.position[0]][self.position[1]])
                    jumplist.append([board[self.position[0]][self.position[1]], "a"])
                    board[self.position[0]][self.position[1]-1] = -1
                    board[self.position[0]][self.position[1]-2] = board[self.position[0]][self.position[1]]
                    board[self.position[0]][self.position[1]] = -1
                    self.position[1] -= 2
            case "s":
                if (self.position[0] < N-2
                        and board[self.position[0]+2][self.position[1]] < 0
                        and board[self.position[0]+1][self.position[1]] > 0):
                    empties.append(board[self.position[0]+1][self.position[1]])
                    empties.append(board[self.position[0]][self.position[1]])
                    jumplist.append([board[self.position[0]][self.position[1]], "s"])
                    board[self.position[0]+1][self.position[1]] = -1
                    board[self.position[0]+2][self.position[1]] = board[self.position[0]][self.position[1]]
                    board[self.position[0]][self.position[1]] = -1
                    self.position[0] += 2
            case "d":
                if (self.position[1] < N-2
                        and board[self.position[0]][self.position[1]+2] < 0
                        and board[self.position[0]][self.position[1]+1] > 0):
                    empties.append(board[self.position[0]][self.position[1]+1])
                    empties.append(board[self.position[0]][self.position[1]])
                    jumplist.append([board[self.position[0]][self.position[1]], "d"])
                    board[self.position[0]][self.position[1]+1] = -1
                    board[self.position[0]][self.position[1]+2] = board[self.position[0]][self.position[1]]
                    board[self.position[0]][self.position[1]] = -1
                    self.position[1] += 2


def print_board(player):
    for i, row, in enumerate(board):
        for col in range(len(row)):
            if ([i,col] == player.position):
                print('X', end='')
            elif (row[col] > 0):
                print('.', end='')
            elif (row[col] == 0):
                print(' ', end='')
            elif (row[col] < 0):
                print('O', end='')
        print('\n')
    print("empties: ", empties)
    print("jumplist: ", jumplist)
    print("valids: ", valids)

def check_loss():
    global valids
    valids = 0
    for i, row in enumerate(board):
        for col in range(len(row)):
            if ((i > 1 and board[i-2][col] < 0 and board[i-1][col] > 0) or 
                (col > 1 and board[i][col-2] < 0 and board[i][col-1] > 0) or 
                (i < N-2 and board[i+2][col] < 0 and board[i+1][col] > 0) or
                    (col < N-2 and board[i][col+2] < 0 and board[i][col+1] > 0)):
                if (board[i][col] > 0):
                    valids += 1
    if (valids == 0):
        game_over(0)


def check_win():
    pegs = 0
    for i, row in enumerate(board):
        for col in range(len(row)):
            if (board[i][col] > 0):
                pegs+= 1
        if (pegs > 1):
            return
    if (pegs == 1):
        game_over(1)


def game():
    player = Player()
    print_board(player)
    print(player.position)
    while True:
        inp = input("move: ")
        if (inp == "q"):
            break
        player.move(inp)
        check_win()
        check_loss()
        system('clear')
        print_board(player)

def game_over(status):
    if (status == 1):
        print("GAME OVER: YOU WON!")
    else:
        print("GAME OVER: YOU LOST!")
    exit()
    

if __name__ == "__main__":
    game()

DFS (optimistically)

I played a couple times to test my new boundary conditions, and then copied over the DFS code from the British version.

Note that in the schematic above the starting position is changed from the center. This is reflected in the following code, and is due to the 36 marble variant being unsolvable from the center starting position.3

N = 7

class PegSolitaire:
    def __init__(self, board, moves, lvl, idx):
        self.board = board
        self.moves = moves
        self.lvl = lvl
        self.idx = idx

    def is_solved(self):
        board = self.board
        pegs = 0
        position = []
        for i, row in enumerate(board):
            for col in range(len(row)):
                if (board[i][col] > 0):
                    position.append([i, col])
                    pegs+= 1
            if (pegs > 1):
                return False
        #if (pegs == 1 and position == [[3,3]]):
        if (pegs == 1):
            return True


    def get_valid_moves(self):
        valids = []
        board = self.board
        for i, row in enumerate(board):
            for col in range(len(row)):
                if (board[i][col] > 0):
                    if (i > 1 and board[i-2][col] < 0 and board[i-1][col] > 0):
                        valids.append([i,col,"w",board[i-1][col]])
                    if (col > 1 and board[i][col-2] < 0 and board[i][col-1] > 0): 
                        valids.append([i,col,"a",board[i][col-1]])
                    if (i < N-2 and board[i+2][col] < 0 and board[i+1][col] > 0):
                        valids.append([i,col,"s",board[i+1][col]])
                    if (col < N-2 and board[i][col+2] < 0 and board[i][col+1] > 0):
                        valids.append([i,col,"d",board[i][col+1]])
        #print("VALID MOVES:", valids)
        #print("MOVES thus far:", self.moves)
        return valids

    def make_move(self, move):
        self.moves.append(move)
        board = self.board
        match move[2]:
            case "w":
                board[move[0]-1][move[1]] = -1
                board[move[0]-2][move[1]] = board[move[0]][move[1]]
                board[move[0]][move[1]] = -1
                move[0] -= 2
            case "a":
                board[move[0]][move[1]-1] = -1
                board[move[0]][move[1]-2] = board[move[0]][move[1]]
                board[move[0]][move[1]] = -1
                move[1] -= 2
            case "s":
                board[move[0]+1][move[1]] = -1
                board[move[0]+2][move[1]] = board[move[0]][move[1]]
                board[move[0]][move[1]] = -1
                move[0] += 2
            case "d":
                board[move[0]][move[1]+1] = -1
                board[move[0]][move[1]+2] = board[move[0]][move[1]]
                board[move[0]][move[1]] = -1
                move[1] += 2
    
    def undo_move(self):
        move = self.moves.pop()
        board = self.board
        #print("POPPED:", move)
        match move[2]:
            case "w":
                board[move[0]+2][move[1]] = board[move[0]][move[1]]
                board[move[0]][move[1]] = -1
                board[move[0]+1][move[1]] = move[3]
            case "a":
                board[move[0]][move[1]+2] = board[move[0]][move[1]]
                board[move[0]][move[1]] = -1
                board[move[0]][move[1]+1] = move[3]
            case "s":
                board[move[0]-2][move[1]] = board[move[0]][move[1]]
                board[move[0]][move[1]] = -1
                board[move[0]-1][move[1]] = move[3]
            case "d":
                board[move[0]][move[1]-2] = board[move[0]][move[1]] 
                board[move[0]][move[1]] = -1
                board[move[0]][move[1]-1] = move[3]


    def encode_board(self):
        # Converts the board into a single integer, assuming a flat list of cells
        return int("".join("1" if cell > 0 else "0" for row in self.board for cell in row), 2)

    def dfs(self, visited=None):
        if visited is None:
            visited = set()  # Initialize the visited set on the first call

        # Encode the board state as a single integer
        board_state = self.encode_board()

        # Check if this encoded board state has already been visited
        if board_state in visited:
            return False

        # Mark the board as visited
        visited.add(board_state)

        # Base case: Check if solved
        if self.is_solved():
            return True

        # Explore each valid move
        for move in self.get_valid_moves():
            #self.print_board()
            self.make_move(move)
            if self.dfs(visited):  # Pass visited set to recursive calls
                return True
            self.undo_move()  # Backtrack if not solved at this depth

        # Optional: Uncomment if you want to remove the state after backtracking
        # visited.remove(board_state)

        return False

    def print_moves(self):
        print(self.moves)
        print(len(self.moves))

    def print_loc(self):
        print("I am at LVL: %2d, and IDX: %2d" % (self.lvl, self.idx))
            
    def print_board(self):
        board = self.board
        for row in board:
            for col in range(len(row)):
                if (row[col] > 0):
                    print('.', end='')
                elif (row[col] == 0):
                    print(' ', end='')
                elif (row[col] < 0):
                    print('O', end='')
            print('\n')

if __name__ == "__main__":
    board = [[ 0,  0,  1,  2,  3,  0,  0],
             [ 0,  4,  5,  6,  7,  8,  0],
             [ 9, 10, 11, 12, 13, 14, 15],
             [16, 17, 18, 19, 20, 21, 22],
             [23, 24, 25, 26, 27, 28, 29],
             [ 0, 30, 31, 32, 33, 34,  0],
             [ 0,  0, 35, 36, -1,  0,  0]]
    game = PegSolitaire(board, [], 0, 0)
    game.dfs()
    game.print_moves()

Algorithmic Analysis

This approach of caching visited board states took me 2 days to discover and it too was facilitated by Durango Bill's analysis of the topic. For many hours I implemented iterative and recursive BFS, DFS and Iterative Deepening DFS's, only to crash my computer (running out of RAM), and get stuck in loops. Eventually, I opt to cache the board state via this ChatGPT 3.5 simple encoding:

    def encode_board(self):
        # Converts the board into a single integer, assuming a flat list of cells
        return int("".join("1" if cell > 0 else "0" for row in self.board for cell in row), 2)

For comparison, employing this visited set strategy on the 32-peg board locates a DFS solution much faster:

python dfs-memory.py  0.20s user 0.03s system 92% cpu 0.255 total

Approx 720 times faster!

Furthermore, for our 36-peg problem we go from an infinite time-complexity to:

python search.py  225.05s user 2.00s system 98% cpu 3:51.33 total

Solution

Once again, our silly program outputs a silly string: [[6, 4, 's', 33], [4, 4, 's', 20], [2, 4, 's', 7], [0, 4, 'd', 2], [1, 4, 'd', 6], [3, 4, 's', 3], [2, 4, 'd', 12], [2, 2, 'd', 10], [2, 3, 'a', 11], [1, 2, 'w', 9], [1, 3, 'd', 18], [0, 3, 'w', 4], [3, 2, 'd', 17], [2, 5, 'w', 21], [2, 4, 'a', 28], [1, 4, 'w', 15], [2, 4, 's', 5], [4, 5, 'd', 13], [4, 3, 'd', 25], [4, 4, 'a', 26], [4, 5, 'd', 29], [3, 5, 'w', 24], [3, 4, 'a', 34], [1, 4, 'w', 1], [1, 3, 'a', 22], [2, 3, 's', 8], [4, 3, 's', 19], [4, 2, 'w', 31], [4, 1, 'a', 35], [4, 2, 'd', 14], [5, 2, 's', 23], [4, 3, 'w', 32], [5, 3, 'd', 16], [6, 3, 's', 30], [6, 2, 'a', 36]] [[6, 4, 's', 32], [4, 4, 's', 19], [2, 4, 's', 7], [0, 4, 'd', 2], [1, 4, 'd', 6], [3, 4, 's', 3], [2, 4, 'd', 12], [2, 2, 'd', 10], [2, 3, 'a', 11], [1, 2, 'w', 9], [1, 3, 'd', 18], [0, 3, 'w', 4], [3, 2, 'd', 17], [2, 5, 'w', 20], [2, 4, 'a', 27], [1, 4, 'w', 15], [2, 4, 's', 5], [4, 5, 'd', 13], [4, 3, 'd', 24], [4, 4, 'a', 25], [4, 5, 'd', 28], [3, 5, 'w', 23], [3, 4, 'a', 33], [1, 4, 'w', 1], [1, 3, 'a', 21], [2, 3, 's', 8], [4, 3, 's', 36], [4, 2, 'w', 30], [4, 1, 'a', 34], [4, 2, 'd', 14], [5, 2, 's', 22], [4, 3, 'w', 31], [5, 3, 'd', 16], [6, 3, 's', 29], [6, 2, 'a', 35]]

So, again we consider a more humane representation: \[\begin{matrix} & & \mathrm{o} & \mathrm{o} & \mathrm{o} & & \\ &\mathrm{o} & \mathrm{o} & \mathrm{o} & \mathrm{o} &\mathrm{o} & \\ \mathrm{o} & \mathrm{o} & \mathrm{o} & \mathrm{o} & \mathrm{o} & \mathrm{o} & \mathrm{o} \\ \mathrm{o} & \mathrm{o} & \mathrm{o} & \mathrm{o} & \mathrm{o} & \mathrm{o} & \mathrm{o} \\ \mathrm{o} & \mathrm{o} & \mathrm{o} & \mathrm{o} & \mathrm{o} & \mathrm{o} & \mathrm{o} \\ &\mathrm{o} & \mathrm{o} & \mathrm{o} & \mathrm{o} & \mathrm{o} & \\ & & \mathrm{o} & \mathrm{o} & . & & \\ \end{matrix}\;\leadsto\;\begin{matrix} & & \mathrm{1} & \mathrm{2} & \mathrm{3} & & \\ &\mathrm{4} & \mathrm{5} & \mathrm{6} & \mathrm{7} &\mathrm{8} & \\ \mathrm{9} & \mathrm{10} & \mathrm{11} & \mathrm{12} & \mathrm{13} & \mathrm{14} & \mathrm{15} \\ \mathrm{16} & \mathrm{17} & \mathrm{18} & \mathrm{19} & \mathrm{20} & \mathrm{21} & \mathrm{22} \\ \mathrm{23} & \mathrm{24} & \mathrm{25} & \mathrm{26} & \mathrm{27} & \mathrm{28} & \mathrm{29} \\ & \mathrm{30} & \mathrm{31} & \mathrm{32} &\mathrm{33} & \mathrm{34} & \\ & & \mathrm{35} & \mathrm{36} & . & & \\ \end{matrix}\]

And trace out the table:

\[\begin{array}{c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c} \mathrm{marble} & \mathrm{33} & \mathrm{13} & \mathrm{3} & \mathrm{1} & \mathrm{5} & \mathrm{7} & \mathrm{11} & \mathrm{9} & \mathrm{14} & \mathrm{18} & \mathrm{4} & \mathrm{12} & \mathrm{16} & \mathrm{28} & \mathrm{15} & \mathrm{20} & \mathrm{3} & \mathrm{26} \\ \hline & \mathrm{24} & \mathrm{29} & \mathrm{26} & \mathrm{34} & \mathrm{22} & \mathrm{19} & \mathrm{8} & \mathrm{2} & \mathrm{12} & \mathrm{35} & \mathrm{26} & \mathrm{23} & \mathrm{18} & \mathrm{36} & \mathrm{30} & \mathrm{26} & \mathrm{19} & \\ \hline \mathrm{move} & \mathrm{d} & \mathrm{d} & \mathrm{d} & \mathrm{r} & \mathrm{r} & \mathrm{d} & \mathrm{r} & \mathrm{r} & \mathrm{l} & \mathrm{u} & \mathrm{r} & \mathrm{u} & \mathrm{r} & \mathrm{u} & \mathrm{l} & \mathrm{u} & \mathrm{d} & \mathrm{r} \\ \hline & \mathrm{r} & \mathrm{l} & \mathrm{r} & \mathrm{u} & \mathrm{l} & \mathrm{u} & \mathrm{l} & \mathrm{d} & \mathrm{d} & \mathrm{u} & \mathrm{l} & \mathrm{r} & \mathrm{d} & \mathrm{u} & \mathrm{r} & \mathrm{d} & \mathrm{l} & \end{array}\]

European Solution
/projects/csp/peg-solitaire/ euro-dfs.gif
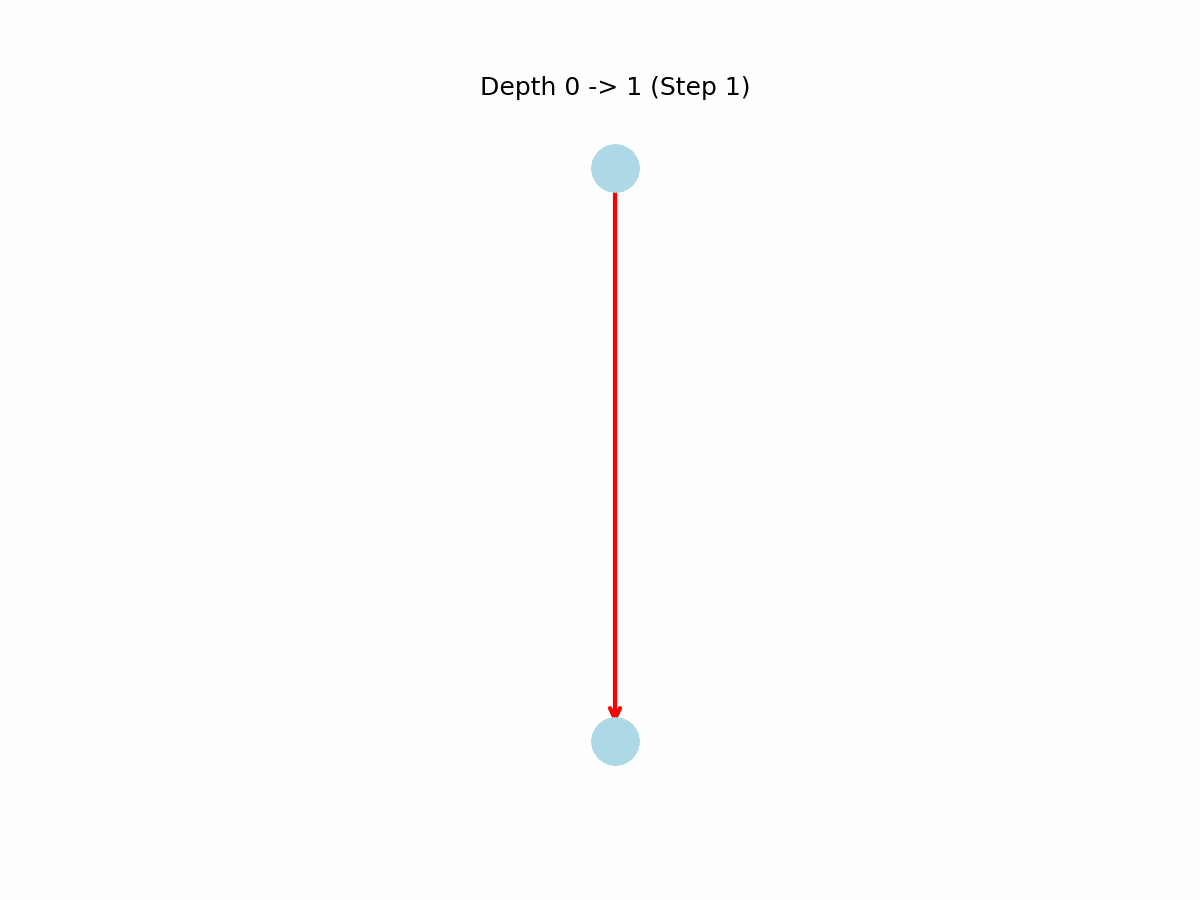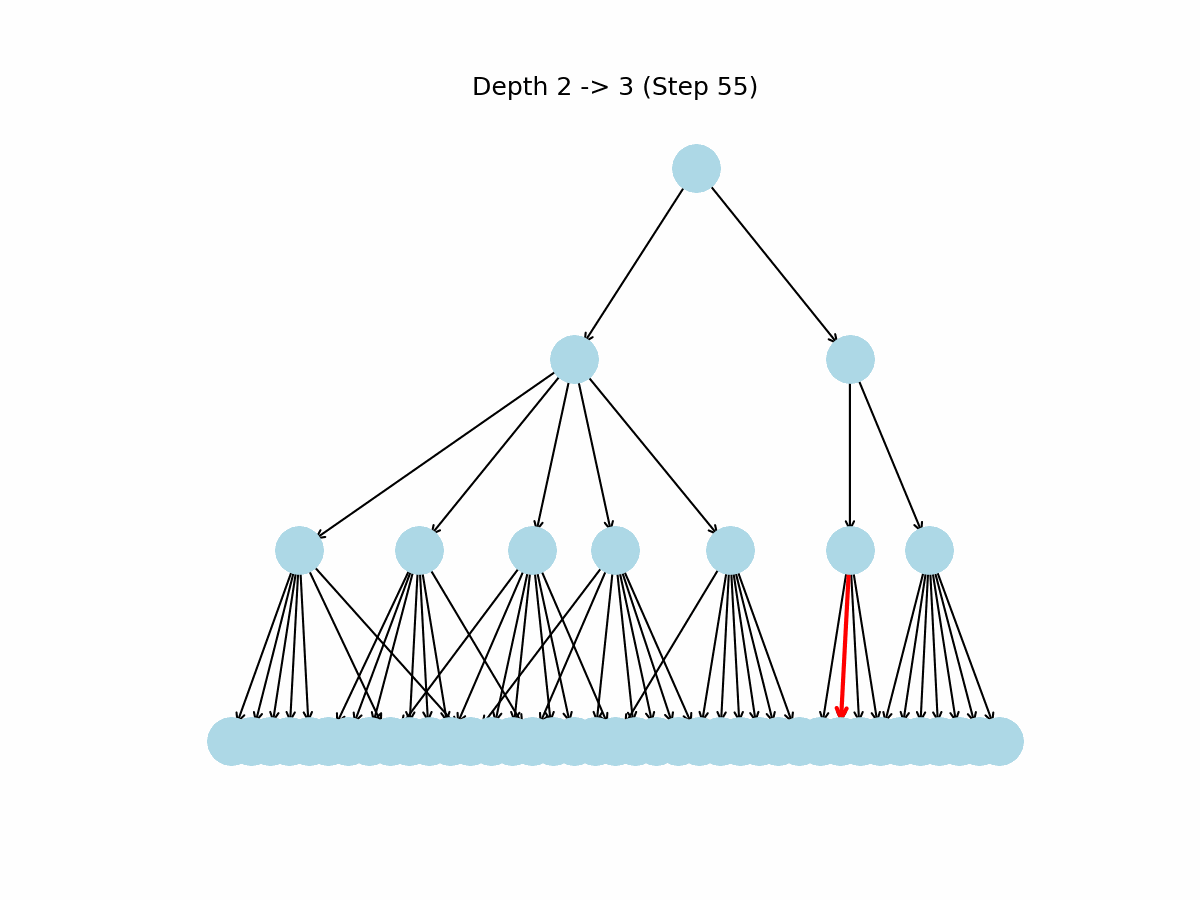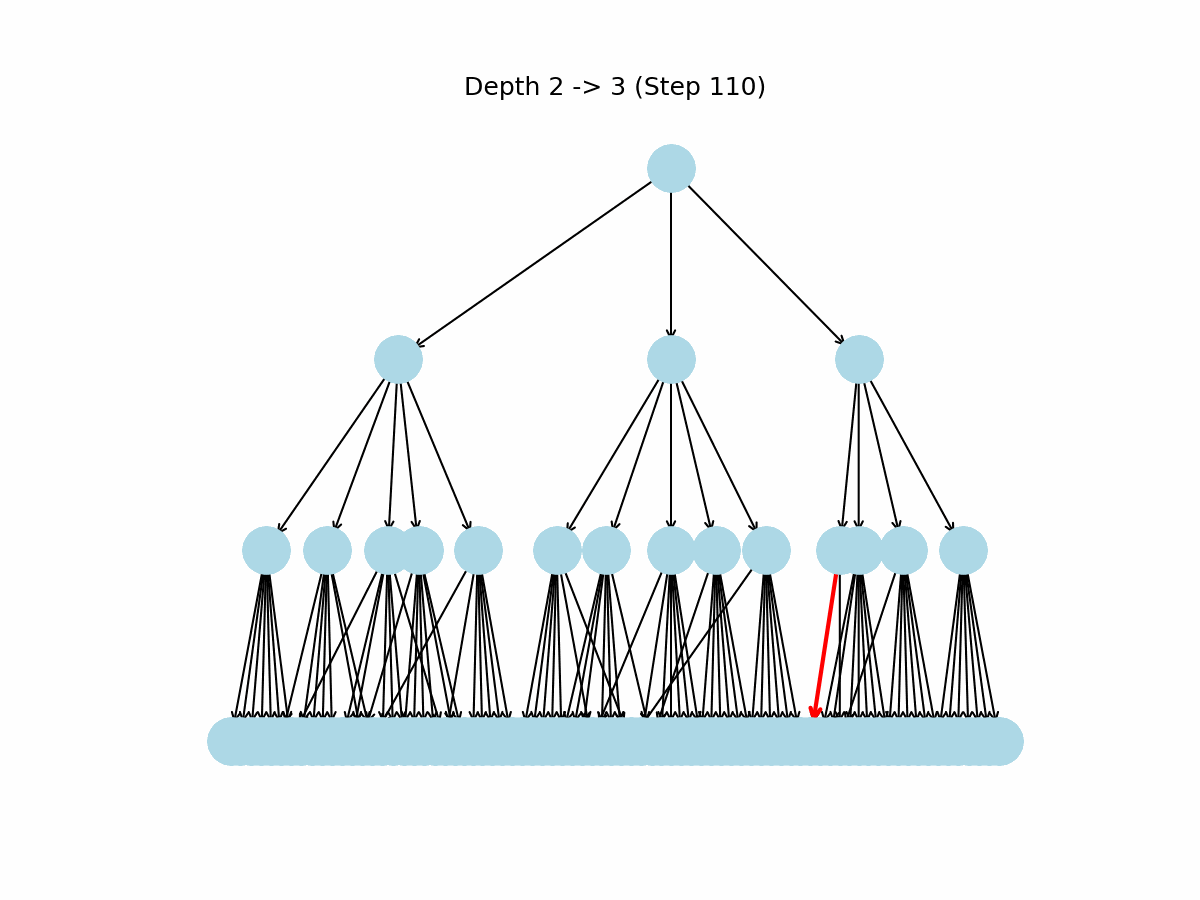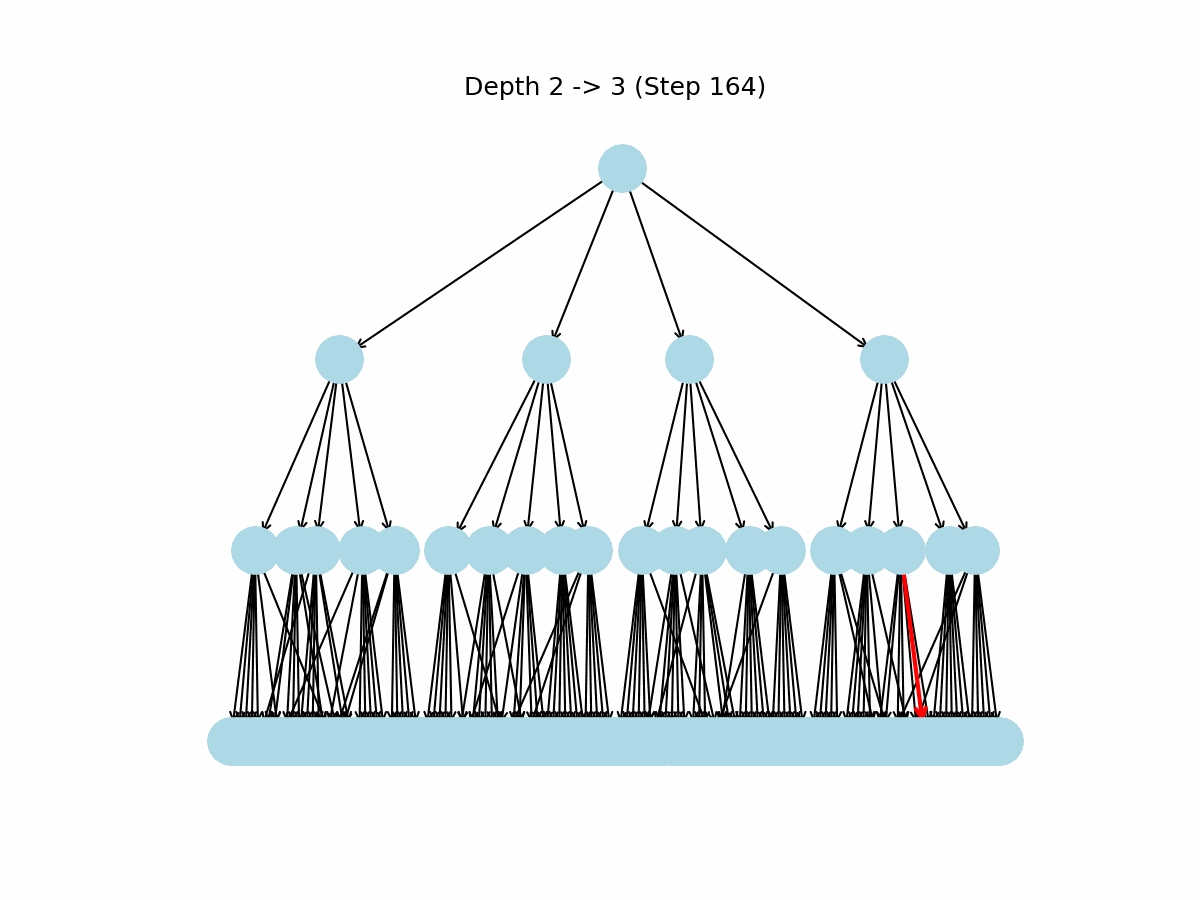
Figure 3: Sensible DFS Gametree

This algorithm produces a far more sensible game-tree as can be observed on the right. The key observation here is that occasionally an edge connects from a node to an identical previously explored node!

Prospectives

  1. Looking forwards, I wish to train a learner to solve this puzzle via reinforcement learning.
  2. I wish to refactor my code into a general purpose CPP implementation such as that which can be found here.

Footnotes

1

with (0,0) being the top left of the board, and (6,6) being the bottom right.

2

(up,down,left,right).

3

see https://en.wikipedia.org/wiki/Peg_solitaire#Strategy for the proof by Hans Zantema